Dancing Links 算法学习小结
文中提及的一些观点和理论,并非全部个人原创,而是自己的总结和心得, 仅供个人学习编程使用!
Dancing Links(DLX),又 被直译为“神奇的舞蹈链”,本质是一个“双向十字循环链表”!是由斯坦福大学的康纳德 E.Knuth在2000年左右提出的一个解决一种NPC问题的算法!对我们acm的竞赛来说,在处理一类搜索问题时,十分有用。
先分享一下学习这种算法比较好的几份资料:
1. 《Dancing Links》 (Donald E. Knuth)本人的论文。英文版的,也有中文的,而且翻译的也很到位: http://sqybi.com/works/dlxcn/#p11#p11
2.《Dancing Links在搜索中的应用》 (momodi)momodi的这篇文章比较系统的讲述了dlx的原理及处理Exact Cover Problem 和 重复覆盖的方法。
依据做过的题目的特点,在简单描述过dlx的插入和删除的方法之后,结合相应的题目,讲一下自己对“完美覆盖(棋盘问题,数独(sudoku)问题,N皇后问题)” 和 “重复覆盖”的理解。
dlx的节点的存储结构:用结构体来表示:
struct node {
int S, C; // size->列链表中节点的总数; column-> 列链表头指针;
int L, R; // left->左向指针, right-> 右向指针; 左右方向
int U, D; // up-> 上向指针, down-> 下向指针;上下方向
};
dlx的节点的删除
void remove(const int&c) {
// column's deleted
d[d[c].L].R = d[c].R;
d[d[c].R].L = d[c].L;
// row's deleted
d[d[c].U].D = d[c].D;
d[d[c].D].U = d[c].U;
}
dlx的节点的恢复
void resume(const int &c) {
// column's resume, d指向的节点要保留原有的信息,
d[d[c].L].R = c;
d[d[c].R].L = c;
// row's resume, d指向的节点要保留原有的信息
d[d[c].U].D = c;
d[d[c].D].U = c;
}
除此之外,为了遍历的方便,要设置一个总的头节点的head!
完美覆盖(精确覆盖)模型
给定一个0-1矩阵,现在要选择一些行,使得一列有且仅有一个 1,如下左:
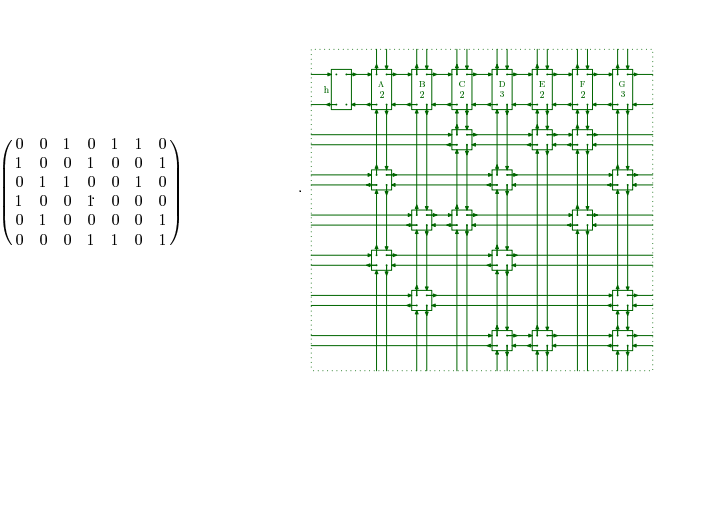
取行集合{1, 4, 5}便可以使得每一列仅有一个1。如果我们把行集合{2, 3, 6}删掉,并用不同的染色将剩余的行中列为1的标记出来,那么就会得到一个一个完全覆盖的board。这也是这个题目的算法的大体思路:任意选择一列(这里我们先选择任意一列,待会再说如何优化),选择为1的一行,然后将该从该行中找出所有的节点值为1的节点,将这些节点所在的列中节点为值为1的行删除掉,这样我们就可以保证选择了改行之后,保证每列中只有一个1。 这样将所有的行试探之后,如果最后存在一种可以使得原矩阵为空的方案,那么就找到一组解。下面简单说一下对优化(即,每次选择剩余列中元素个数最少的来删除)的理解,
我们优化的出发点是选择尽量少的行找到一组可行解,按照我们上面的思路就是选择一行的同时尽量多的删除其它的行。由此,列的值(多少代表着影响的行数)大的删掉的行数也就越多,那么就更大的可能接近可行解。(只是论述,缺乏严密的数学证明)(更为具体的分析,参见momodi的论文P4,下面附上一段伪代码,帮助理解)
A is the matrix of the 0-1.
if (A is empty) {
\\A is the 0 - 1 matrix.
the problem is solved;
return;
}
choose a column, c,that is unremoved and has fewest elements. ..(1)
remove c and each row i that A[i][c] == 1 from matrix A;...(2)
for (all row, r, that A[r][c] == 1) {
include r in the partial solution.;
for each j that A[r][j] == 1 {
remove column j and each row i
that A[i][j] == 1 from matrix A. ...(3)
}
repeat this algorithm recursively on the reduced matrix A.
resume all column j and row i that was just removed;...(4)
}
resume c and i we removed at step(2) ...(5);
完美覆盖的cpp实现。
// resumecolumn c and all row i that a[i][c] = 1;
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
for (int j = d[i].L; j != i; j = d[j].L) {
d[d[j].C].S++;
d[d[j].U].D = j;
d[d[j].D].U = j;
}
}
d[d[c].R].L = c;
d[d[c].L].R = c;
}
// the k'th step of the deepth first search;
bool dfs(const int &k) {
if (d[head] == head) {
return true;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
remove(c);
for (int i = d[c].D; i != c; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
remove(d[j].C);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(d[j].C);
}
}
resume(c);
return false;
}
重复覆盖模型:在0-1矩阵中选择最少的行,是的每一列至少有一个1.
该问题可以想象成二分图的支配集问题的模型:从X集合选择最少的点,是的能否覆盖住Y集合所有的点。(当然X与Y集合是有边(映射)关系的)。
把这个问题和上面的完美覆盖结合起来看,我们就会发现不同的地方就是,上面红色标出的那句话,实际上也是如此。能够想到的一个中直观的搜索方法是:我们每次选择任意选一列,然后从该列选择任意一行,同时将列值为1的节点所在的列删掉(这里不再是将列上值为1的节点所在的行删掉,因为不再要求列值为1)。如果,最后的所有的列都删掉了,那么就可以说找到一组可行解。
这个题目的做法是用迭代加深的启发式搜索(ID_A*)。那么,我们来说一下启发函数的设计。
int h() {
int ret = 0;
memset(use, 0, sizeof(use));
for (int t = d[head].R; t != head; t = d[t].R) {
if (use[t] == false) {
use[t] = true; ret ++;
for (int i = d[t].D; i != t; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
use[d[j].C] = true;
}
}
}
}
return ret;
}
启发函数的值 = 按一定的规则选择列,是的所有的列都被选择需要的最少的行数。(这里的按一定的规则是说,每次开始选择列的时候都遵守一个规则)。说明估价函数(f() = g() + h())发函数的正确性,我们只需要说明两点:1. f()满足单调不减的特性; 2. h()是相容的,也就是说,设pres, curs 为前一个状态和当前状态,weight为状态转移代价,那么h(pres) <= curs + weight。 按通常的dfs的估价函数设计的方法,去实际代价函数g() = depth of the search. 那么 g()函数值每只增加一个单位“1”。对于h()函数,按照f的不递减的特性,需要满足每次减少的最大值为“1"才可。 如果按照我们我们上面启发函数的设计原则,每次计算的时候记录下计算估价函数值时用到的列,那么,对于当前的此次计算挂架函数值,会出现两种情况,一是,原来记录下的列有被删除的(每次只能删除一个原来记录的列,因为,记录的列之间是没有关系的),这样h()的函数值减小一;二是,原来记录的列没有被删除的,这样h()的函数值保持不变。由此,weight = 0 或 1,h() 函数是相容的,f() = g() + h() 满足单调不递减的特性。
简单的来说,对于重复覆盖,我们只删除列,不删除行。由此得到以下的cpp重复覆盖的代码(供参考)
void remove(const int &c) {
for (int i = d[c].D; i != c; i = d[i].D) {
d[d[i].R].L = d[i].L;
d[d[i].L].R = d[i].R;
}
}
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
d[d[i].R].L = i;
d[d[i].L].R = i;
}
}
bool dfs(const int &k) {
if (k + h() >= limit) {
return false;
}
if (d[head].R == head) {
if (k < limit) limit = k;
return true;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return false;
}
int astar() {
limit = h();
while(dfs(0) == false) limit++;
return limit;
}
对于ID_A*,我个人比较喜欢下面的这种实现方法:
int dfs(const int &k) {
if (k + h() > limit) {
return k + h();
}
if (d[head].R == head) {
flg = true;
//if (k < limit) limit = k;
return k;
}
// printf("k = %d\n", k);
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
int nxt = inf, tmp;
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
tmp = dfs(k + 1);
if (flg == true) {
return tmp;
}
nxt = min(nxt, tmp);
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return nxt;
}
- 无匹配
Copyright © 2007
2011年8月23日 18:26
请问为什么精确覆盖和重复覆盖的remove和resume用法不一样呢,理论上感觉只要把精确覆盖的remove和resume修改了可以保证主体不动来适应重复覆盖,可是实际上却行不通,这个问题很困扰我
2013年12月26日 01:56
@icek: 我是来膜拜的
2013年12月26日 15:15
@rpk74m: 囧了,好多年前的回复了
2023年4月23日 15:23
crediblebh