文中提及的一些观点和理论，并非全部个人原创，而是自己的总结和心得， 仅供个人学习编程使用！
LBOY: 双向广度优先搜索，简单的讲就是从初始节点和目标节点两个方向向中间进行搜索，如果是按层次遍历，那么这样他们第一次相遇的时候，肯定是最优的。这里的按层次遍历，我们可以理解为一个点绕一个固定的圆心来画圆弧，每次圆弧所在圆的半径增加一，这样的一个圆弧就是广搜，两个圆弧就是双广。
下面让我们来看看问什么非得是按层次搜索。
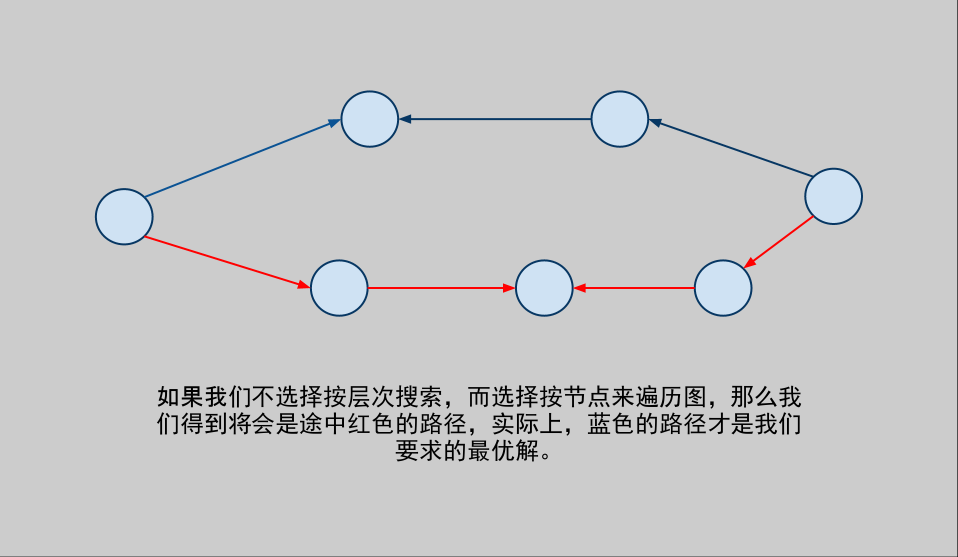
下面给出一段伪代码：（摘抄至某ppt）
Bool DBFS();
Begin
Queue Q[2]; Map M[2];
Q[0].Push(start); M[0][start] = 1;
Q[1].Push(end); M[1][end] = 1;
Step := 0; Idx := 0;
while(!Q[0].Empty() || !Q[1].Empty());
Begin
Idx = Step & 1;
Cnt := Q[Idx].Size();
While(Cnt--);
Begin
Cur = Q[Idx].front();
Q[Idx].Pop();
if (M[Idx^1].Find(Cur) != M.End) then
return True;
for each Ext = Extend(Cur)
Begin
if (M[Idx].Find(Ext) == M.end()) then
Q[Idx].Push(Ext);
M[Idx][Ext] = True;
End;
End
Step++;
End;
Return False;
End;
上面的代码中的Step是很有用的, 不仅记录了搜索树的深度，还通过交替搜索判断是那个队列进行操作。
Solitaire
LBOY: 一个棋盘上给定4个旗子，每个棋子可以往相邻的四个方向移动一步，或者往相邻方向存在棋子的格子移动两步。给定棋子的初始状态 和 目标状态，问能否从初始状态到达目标状态。如果可以的话，给出最小的步数。
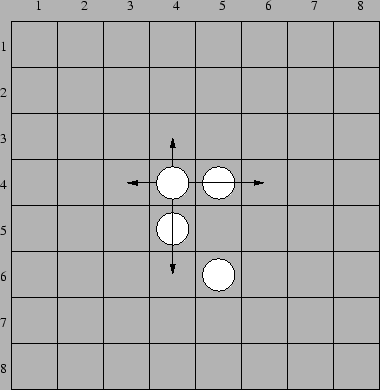
双广的题目，一般是比较明确的，可以找到给定问题的一个初始状态和一个目标状态（多目标，多初始的可以增加源点汇点）。以这个一个题目为例说一下双广的求解的大体过程。
一个棋子往某一方向最多移动两步，因此，要判断这个方向是否可行。
题目总共有8*8个格子，那么我们可以用一个64位整型来保存每个状态，这需要hash来判重或者通过set，map 也可以，我个人习惯set.
根据刘的黑书的提示，双广A*的算法的正确性未知，所以不建议增设启发函数，当然这个题目可以用A*来做，但是，可以考虑用来做毕业设计的题目。
贴一些可爱又可恶的代码吧！
#include <iostream>
#include <set>
#include <queue>
using namespace std;
#define u64 unsigned __int64
struct node {
int x[4], y[4], s;
u64 state;
void out() {
printf("stp = %d: ", s);
for (int k = 0; k < 4; k++) {
printf("(%d, %d), ", x[k], y[k]);
}
putchar('\n');
for (int k = 63; k >= 0; k--) {
putchar(state & ((u64)1 << k) ? '1':'0');
}
putchar('\n');
}
}init, goal, cur, tmp;
queue<node> q[2];
set<u64> sq[2];
int d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
inline u64 num(int x, int y) {
return ((u64)1 << ((x-1)*8 + (y-1)));
}
inline bool islegal(int x, int y) {
return 1 <= x && x <= 8 && 1 <= y && y <= 8;
}
bool dbfs() {
if (init.state == goal.state) {
return true;
}
if (!sq[0].empty()) sq[0].clear();
if (!sq[1].empty()) sq[1].clear();
while(!q[0].empty()) q[0].pop();
while(!q[1].empty()) q[1].pop();
q[0].push(init);
sq[0].insert(init.state);
q[1].push(goal);
sq[1].insert(goal.state);
int idx = 0, cnt, stp[2] = {0,0};
while(!q[idx].empty() || !q[idx^1].empty()) {
cnt = q[idx].size();
while(cnt--) {
cur = q[idx].front(); q[idx].pop();
stp[idx] = cur.s + 1;
for (int i = 0; i < 4; i++) {
for (int k = 0; k < 4; k++) {
tmp = cur;
tmp.x[i] = cur.x[i] + d[k][0];
tmp.y[i] = cur.y[i] + d[k][1];
tmp.state ^= num(cur.x[i], cur.y[i]);
tmp.s = cur.s + 1;
if (islegal(tmp.x[i], tmp.y[i]) == true) {
if ((cur.state & num(tmp.x[i], tmp.y[i])) != 0) {
tmp.x[i] += d[k][0];
tmp.y[i] += d[k][1];
if (islegal(tmp.x[i], tmp.y[i]) == true) {
if ((cur.state & num(tmp.x[i], tmp.y[i])) == 0) {
tmp.state |= num(tmp.x[i], tmp.y[i]);
if (sq[idx^1].find(tmp.state) != sq[idx^1].end()) {
return tmp.s + stp[idx^1] <= 8;
}
if (sq[idx].find(tmp.state) == sq[idx].end()) {
sq[idx].insert(tmp.state);
q[idx].push(tmp);
}
}
}
} else {
tmp.state |= num(tmp.x[i], tmp.y[i]);
if (sq[idx^1].find(tmp.state) != sq[idx^1].end()) {
return tmp.s + stp[idx^1] <= 8;
}
if (sq[idx].find(tmp.state) == sq[idx].end()) {
sq[idx].insert(tmp.state);
q[idx].push(tmp);
}
}
}
}
}
}
if (stp[idx] > 4) return 0;
idx ^= 1;
}
return false;
}
int main() {
//freopen("in.in", "r", stdin);
//freopen("out.out", "w", stdout);
while(scanf("%d %d", init.x, init.y) != EOF) {
init.state = num(init.x[0], init.y[0]);
for (int k = 1; k < 4; k++) {
scanf("%d %d", init.x + k, init.y + k);
init.state |= num(init.x[k], init.y[k]);
}
goal.state = 0;
for (int k = 0; k < 4; k++) {
scanf("%d %d", goal.x + k, goal.y + k);
goal.state |= num(goal.x[k], goal.y[k]);
}
init.s = goal.s = 0;
//init.out(); goal.out();
puts(dbfs() ? "YES":"NO");
}
return 0;
}
小结：双广的题目正如前面讲的那样，起始和目标状态是比较明确的。选择双广的前提，是状态的数量很多，但是，A*或者IDA*的启发函数有不好想的前提下。
下面给出一个我做的失败的题目，测试数据是都过了，不过没有在规定的时间内跑出测试数据，我自己的机子是可以的！我打表（实际上是人肉的测试数据）代码6k+.没兴趣优化，优化，过去应该没问题的。
#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
using namespace std;
const int maxn = 16;
const int maxs = 1<<24;
const int Size = 1<<18;
char W, H, n;
char mat[maxn][maxn];
char dir[5][2] = {
{0, 0}, {-1, 0}, {0, 1}, {1, 0}, {0, -1}
};
struct node {
int st, d;
node(int st = 0, int d = 0):st(st), d(d) {}
void out() {
printf("%d, %d, %d\n", d&7, (d>>3)&7, (d>>6)&7);
printf("(%d, %d), ", st & 15, (st >> 4) & 15);
printf("(%d, %d), ", (st >> 8) & 15, (st >> 12) & 15);
printf("(%d, %d)\n", (st >> 16) & 15, (st >> 20) & 15);
}
}init, goal, cur;
struct queue {
int beg, end;
node key[Size+1];
node front() {
return key[beg];
}
void push(node k) {
key[end] = k;
end = (end+1) & (Size-1);
}
void pop() {
beg = (beg + 1) & (Size-1);
}
bool empty() {
return beg == end;
}
void clr() {
beg = end = 0;
}
int size() {
return end - beg;
}
}q[2];
unsigned char h[2][maxs];
bool flg[2][3];
int num[5][3];
inline void deal(int &sta, int x, int y, int id) {
switch(id) {
case 0: sta += x + (y << 4); break;
case 1: sta += (x << 8) + (y << 12); break;
case 2: sta += (x << 16) + (y << 20); break;
}
}
inline bool islegal(int x, int y) {
return !(x < 0 || x >= H || y < 0 || y >= W) && mat[x][y] != '#';
}
inline bool opp(bool idx, int d, int da, int db, int dc) {
char ret = 0;
if (flg[idx][0] == true && (d&7) && da) {
if (abs( (d&7) - da) != 2) {
return false;
}
ret++;
}
if (flg[idx][1] == true && ((d>>3) & 7) && ((db>>3)&7)) {
if (abs( ((d>>3) & 7) - ((db>>3)&7)) != 2) {
return false;
}
ret++;
}
if (flg[idx][2] == true && ((d>>6) & 7) && ((dc>>6)&7) ) {
if (abs( ((d>>6) & 7) - ((dc>>6)&7)) != 2) {
return false;
}
ret++;
}
return ret == 3;
}
inline bool same(int x1, int y1, int x2, int y2) {
return x1 == x2 && y1 == y2;
}
int dbfs() {
memset(h, 0, sizeof(h));
//while(!q[0].empty()) q[0].pop();
//while(!q[1].empty()) q[1].pop();
q[0].clr(); q[1].clr();
q[0].push(init); h[0][init.st] = 1;
q[1].push(goal); h[1][goal.st] = 1;
bool idx = 0;
int cnt, nxt;
int xa, ya, xb, yb, xc, yc;
int a, b, c, ta, tb, tc, da, db, dc;
int ax, ay, bx, by, cx, cy;
while(!q[0].empty() || !q[1].empty()) {
cnt = q[idx].size(); // printf("idx = %d\n", idx);
while(cnt--) {
cur = q[idx].front(); q[idx].pop();// cur.out();
nxt = 0;
ax = cur.st & 15; ay = (cur.st >> 4) & 15;
bx = (cur.st >> 8) & 15; by = (cur.st >> 12) & 15;
cx = (cur.st >> 16) & 15; cy = (cur.st >> 20) & 15;
for (a = 0; a < 5; a ++) {
xa = ax + dir[a][0];
ya = ay + dir[a][1];
if (flg[idx][0] == false || islegal(xa, ya) == true) {
if (flg[idx][0] == true) {
ta = xa + (ya << 4);
da = a;
} else {
ta = 0;
da = 0;
}
for (b = 0; b < 5; b++) {
xb = bx + dir[b][0];
yb = by + dir[b][1];
if (flg[idx][1] == false || islegal(xb, yb) == true) {
if (flg[idx][1] == true) {
tb = (xb << 8) + (yb << 12);
db = b << 3;
if (flg[idx][0] == true) {
if (same(xa, ya, xb, yb)) {
continue;
}
if (same(xa, ya, bx, by) && same(xb, yb, ax, ay)) {
continue;
}
}
} else {
tb = 0;
db = 0;
}
for (c = 0; c < 5; c++) {
xc = cx + dir[c][0];
yc = cy + dir[c][1];
if (flg[idx][2] == false || islegal(xc, yc) == true) {
if (flg[idx][2] == true) {
tc = (xc << 16) + (yc << 20);
dc = c<<6;
if (flg[idx][0] == true) {
if (same(xa, ya, xc, yc)) {
continue;
}
if (same(xa, ya, cx, cy) && same(xc, yc, ax, ay)) {
continue;
}
}
if (flg[idx][1] == true) {
if (same(xb, yb, xc, yc)) {
continue;
}
if (same(xb, yb, cx, cy) && same(xc, yc, bx, by)) {
continue;
}
}
} else {
tc = 0;
dc = 0;
}
if (!(da || db || dc)) {
continue;
}
if (opp(idx, cur.d, da, db, dc)) {
continue;
}
nxt = ta + tb + tc;
if (h[idx^1][nxt] != 0) {
return h[idx^1][nxt] + h[idx][cur.st]-1;
}
if (h[idx][nxt] == 0) {
h[idx][nxt] = h[idx][cur.st] + 1;
q[idx].push(node(nxt, da + db + dc));
}
}
}
}
}
}
}
}
idx ^= 1;
}
return -1;
}
int main() {
//freopen("in.in", "r", stdin);
// freopen("out.out", "w", stdout);
int a[] = { 51, 215,108,108,316,98,17,66, 74,70};
int ca = 0;
while(scanf("%d %d %d", &W, &H, &n) != EOF) {
if (!(W || H || n)) break;
init = node(0, 0);
goal = node(0, 0);
memset(flg, false, sizeof(flg));
for (int i = 0; i < H; i++) {
getchar(); gets(mat[i]);
for (int j = 0; j < W; j++) {
if ('a' <= mat[i][j] && mat[i][j] <= 'c') {
flg[0][mat[i][j] - 'a'] = true;
deal(init.st, i, j, mat[i][j] - 'a');
}
if ('A' <= mat[i][j] && mat[i][j] <= 'C') {
flg[1][mat[i][j] - 'A'] = true;
deal(goal.st, i, j, mat[i][j] - 'A');
}
}
}
printf("%d\n", a[ca++]);
//init.out(); goal.out();
//printf("%d\n", dbfs());
}
return 0;
}
Tags:
上一节简单的描述了A*和IDA*的基本理论，这节针对具体的题目进行分析，重点讲一下启发函数的构造。
八数码问题
启发函数的设计，一般有两种设计思路，可以证明，这两种思路都可以找到最优解。
一种是Diff ( Status a, Status b )，其返回值是a 和b状态相应位置上数字（空格除外）不同的次数。另一种比较经典的是曼哈顿距离Manhattan ( Status a, Status b )，其返回的是各个数字（除却空格）从状态a的位置到状态b的相应位置的最短曼哈顿距离的和。要论证启发函数设计是否可行，要考虑两个条件，一是，h(s) <= h(t) + w(s, t)；二是，f(s) <= f(t)，即f(x)是单调的函数。
对于第一种启发函数的设计思路：每次X标记的位置和周围的四个位置交换，会有两种可能，要么，x标记的返回b状态指示的位置，w(s, t) = 1;要么,w(s, t) = 0;，也就是说h的值每次最多减小1个单位，而去实际代价为搜索树的深度，那么g值每次增加1，那么估价函数f（）= g() + h() 要么增加1，要么不变。所以可以找到最优解。
对于第二种启发函数的设计思路：每次X标记的位置和周围的四个位置交换，会有两种可能，要么，x标记的接近最终的位置一步，w(s, t) = 1;要么,不变或者远离一步，w(s, t) <= -1,也就是说h的值每次最多减小1个单位，而去实际代价为搜索树的深度，那么g值每次增加1，那么估价函数f（）= g() + h()每次可能不变，或者增加1或2，所以可以找到最优解。
搜索问题的优化，一般从下面三种情况考虑，
- Hahs() 判重，这里主要是避免重复搜索，也是搜索里面最为重要的一种剪枝方法。
- 可行性剪枝，判断当前状态能否到达最终的状态。（个人把启发搜索咱归为此类）
- 最优性剪枝，这里主要在深度优先搜索中用到，因为dfs第一次到达目标状态不一定是最优的。（迭代加深的除外）
- 上下界剪枝，这种剪枝方法主要在博弈搜索里面用到。
上面的剪枝优化我们要用到Hash()判重，判重就要记录下所有的位置，并判定当前状态是否已经到达过。这个题目的判重有点麻烦。总共有N!种状态，一般我们要采用hash判重或者set判重，题目中给定的N=9， N! = 40320. 那么我们可以用简单的H[]判重。判重的方法：把当前的board的每个位置上的数排列起来，看成一个序列，判定这些数在N!中是排第几大的一个数。例如789123456对应排列中的第几大？ num(789123456) = 6 * 8！+ 6 * 7! + 6 * 6! + 0*5! + 0*4!+0*3!+0*2!+0*1!+0*0!;这也就是康托展开式。
int Hash(char *board, int n = 9) {
int ret = 0, tmp;
for (int i = 0; i < n-1; i++) {
tmp = 0;
for (int j = i + 1; j < n; j++) {
tmp += board[j] < board[i];
}
ret += frc[ n- i - 1 ] * tmp;
}
return ret;
}
void rHash(char *board, int val, int n = 9) {
int i, x, j, k, b[9];
memset(b, 0, sizeof(b));
for (i = 1; i <= n; i++) {
x = val / frc[n - i];
val %= frc[n - i];
for (j = 1, k = 0; k <= x; j++) {
if (b[j] == 0) k++;
}
b[--j] = 1;
board[i-1] = j;
}
}
有了上面的知识，这个题目就可以0msAC了，数据比较弱。link: http://poj.org/problem?id=1077
#include <iostream>
#include <queue>
using namespace std;
const int maxn = 362880;
int frc[9], goal[9][2];
int f[maxn], d[maxn];
int h(char board[]) {
int ret = 0, k;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
k = i * 3 + j;
if (board[k] != 8) {
ret += abs(i - goal[ board[k] ][0]);
ret += abs(j - goal[ board[k] ][1]);
}
}
}
return ret;
}
int Hash(char *board, int n = 9) {
int ret = 0, tmp;
for (int i = 0; i < n-1; i++) {
tmp = 0;
for (int j = i + 1; j < n; j++) {
tmp += board[j] < board[i];
}
ret += frc[ n- i - 1 ] * tmp;
}
return ret;
}
struct node {
char board[10];
int space, val;
bool operator < (const node &p) const {
return f[val] > f[p.val];
}
};
node init;
bool color[maxn];
priority_queue<node> open;
int par[maxn];
int stp[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int path[maxn];
int ans[maxn], n;
void printPath() {
n = 0;
int u = n = 0;
do {
ans[n++] = path[u];
u = par[u];
} while(par[u] != -1);
while(n--) {
switch(ans[n]) {
case 0: putchar('u'); break;
case 1: putchar('d'); break;
case 2: putchar('l'); break;
case 3: putchar('r'); break;
default: puts("Error");
}
}
}
inline bool islegal(int x, int y) {
return !(x < 0 || x > 2 || y < 0 || y > 2);
}
void astar() {
while(!open.empty()) open.pop();
memset(color, 0, sizeof(color));
memset(path, 0, sizeof(path));
int u, v;
int x1, y1, x2, y2;
node cur, tmp;
u = Hash(init.board);
f[u] = h(init.board);
d[u] = 0; par[u] = -1;
init.val = u;
color[u] = 1;
open.push(init);
while(!open.empty()) {
cur = open.top(); open.pop();
if (cur.val == 0) {
printPath();
return;
}
u = cur.val;
x1 = cur.space / 3;
y1 = cur.space % 3;
for (int k = 0; k < 4; k++) {
x2 = x1 + stp[k][0];
y2 = y1 + stp[k][1];
if (islegal(x2, y2) == true) {
tmp = cur;
tmp.space = x2 * 3 + y2;
swap(tmp.board[tmp.space], tmp.board[cur.space]);
v = Hash(tmp.board); tmp.val = v;
if (color[v] == 1 && d[u] + 1 < d[v]) {
path[v] = k;
f[v] -= d[v] - d[u] - 1;
d[v] = d[u] + 1;
par[v] = u;
open.push(tmp);
}
if (color[v] == 0) {
path[v] = k;
d[v] = d[u] + 1;
f[v] = d[v] + h(tmp.board);
par[v] = u;
open.push(tmp);
color[v] = 1;
}
}
}
}
puts("unsolvable");
}
int main() {
//freopen("in.in", "r", stdin);
for (int k = frc[0] = 1; k < 9; k++) {
frc[k] = frc[k-1] * k;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
goal[i*3 + j][0] = i;
goal[i*3 + j][1] = j;
}
}
char digit[2];
for (int k = 0; k < 9; k++) {
scanf("%s", digit);
if (digit[0] == 'x') {
digit[0] = '9';
init.space = k;
}
init.board[k] = digit[0] - '1';
}
astar();
return 0;
}
The Rotation Game
问题概述：片面上放置24个小木块，每个木块上都有1~3中的一个数字（如上图）ABCDEFG代码一趟7个数字是可以样字母标记的箭头方向移动的，移动的方式是循环的，也就是，A趟的第一个字母可以移动到A趟的最后一个字母位置，A趟其它的字母依次向前移动一个字符。问题：用最少的次数移动八趟，使得中间的八个方格的数字相同，并且要求字典序最小（字典序最小可以用ABCDEFG的方式移动）
问题分析：题目没有告诉最多移动的次数，因此普通的dfs存在危险，可能陷入无限深的搜索。题目说明了必有解，因此，可以用刚学的IDA*来解决这个问题。其余的不多说，说一下启发函数的正确性：
启发函数的值：设置为8-已在中间八个位置的最多的数的个数。对于A*算法的第一个必须条件是显然成立的。我们在移动某某一趟的时候，要么是的中间八个数字中相同的个数多一个，要么少一个，也就是说至多减少一个，而深度增加了一个，因此总的f的值最大只能和移动前的父节点相同。因此，满足两个条件，这个启发函数是可行的，即原问题可以功过这种估价函数找到最优解。
#include <iostream>
using namespace std;
int board[24];
int map[8][7] = { // ABCDEFG 对应一趟的block的下标
{0, 2, 6, 11, 15, 20, 22},
{1, 3, 8, 12, 17, 21, 23},
{10, 9, 8, 7, 6, 5, 4},
{19, 18, 17, 16, 15, 14, 13},
{23, 21, 17, 12, 8, 3, 1},
{22, 20, 15, 11, 6, 2, 0},
{13, 14, 15, 16, 17, 18, 19},
{4, 5, 6, 7, 8, 9, 10}
};
int opp[8] = {5, 4, 7, 6, 1, 0, 3, 2}; // A<->F,B<->E,C<->H,D<->G
int goal[8] = {6, 7, 8, 11, 12, 15, 16, 17}; // 中间八个位置坐标
char ch[8] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};
int h(int board[]) { // 启发函数的值：设置为8-已在中间八个位置的最多的数的个数
int cnt[3] = {0, 0, 0}, ret = 0;
for (int i = 0; i < 8; i++) {
cnt[ board[ goal[i] ] - 1 ]++;
}
return 8 - max(cnt[0], max(cnt[1], cnt[2]));
return ret;
}
void change(int idx) {
int tmp = board[ map[idx][0] ];
for (int i = 0; i < 6; i++) {
board[ map[idx][i] ] = board[ map[idx][i+1] ];
}
board[ map[idx][6] ] = tmp;
}
bool flg;
int ans[10000], bound;
int dfs(int dv, int pre) {
int hv = h(board);
if (hv + dv > bound) {
return hv + dv;
}
if (hv == 0) {
flg = true;
return dv;
}
int next_bound = 1<<30;
for (int k = 0; k < 8; k++) {
if (opp[k] == pre) {
continue;
}
ans[dv] = k;
change(k);
int new_bound = dfs(dv + 1, k);
if (flg) {
return new_bound;
}
next_bound = min(next_bound, new_bound);
change(opp[k]);
}
return next_bound;
}
bool id_astar() {
flg = false;
bound = h(board);
if(bound == 0) {
return false;
}
while(!flg && bound < 1000) {
bound = dfs(0, -1);
}
return flg;
}
int main() {
//freopen("in.in", "r", stdin);
while(scanf("%d", board+0) && board[0]) {
for (int k = 1; k < 24; k++) {
scanf("%d", board + k);
}
if(id_astar() == false) {
printf("No moves needed\n%d\n", board[6]);
continue;
}
for (int i = 0; i < bound; i++) {
putchar( ch[ ans[i] ]);
}
printf("\n%d\n", board[6]);
}
return 0;
}
小结：以上两个题目为A*模型和IDA*模型的基本应用，就是为了熟悉一下两个代码。下面的题目需要点时间思考的。
Booksort
问题概述：给定编号为1..N的一行书架，放着编号为1…N的混乱放置的书，先可以进行插排，问能否在4次包含4次以内 书的数的编号为1…N.
问题提分析：题目告诉了最多操作的次数，进行dfs的操作也应该是可以的，4^16次方的复杂度，需要慎重考虑，需要强有力的剪枝。用IDA*来解决这个问题是完全可以的。说一下启发函数的正确性：
启发函数的值：左侧的书和当前的书放置错误的数目。
对于A*算法的第一个必须条件是显然成立的。现在说明第二个条件的正确性，[0. a-1] [a, b] [b+1, c][c+1, n-1] 我们将元序列划分成4段（因为每次移动的可能为一个子序列），这样如果book[a-1] + 1== book[a] 且book[b] + 1 == book[b+1] 且book[c] + 1 == book[n-1]. 那么h的值最多将减少3. 而如果记实际代价函数为g = depth.那么是不相容的，不能满足第二个条件，这时我们知道深度每次是增加1的，如果乘以3，即g = 3*depth. 那么由f=g+h.可知，f仍然满足单调递增的特性，即满足第二个条件。
知道了上面启发函数的设计方法，这个题目就很简单了！下面分享我的代码（启发函数的设计思路<黑皮书》P169）
#include <iostream>
using namespace std;
int shelf[16], n;
int h(int shelf[]) {
int ret = 0;
for (int i = 1; i < n; i++) {
ret += shelf[i-1] + 1 != shelf[i];
}
return ret;
}
int t[16];
void change(int a, int b, int c) { //[a, b], [b+1, c]
int m = 0;
for (int k = b+1; k <= c; k++) {
t[m++] = shelf[k];
}
for (int k = a; k <= b; k++) {
t[m++] = shelf[k];
}
for (int k = a; k <= c; k++) {
shelf[k] = t[k-a];
}
}
int bound, flg;
int dfs(int dv) {
int hv = h(shelf);
if (hv + 3*dv > 3*bound) {
return (hv + 3*dv + 2)/3;
}
if (hv == 0) {
flg = true;
return dv;
}
int nxt_bound = 5, new_bound;
for (int i = 0; i < n-1; i++) {
for (int j = i; j < n-1; j++) {
for (int k = j + 1; k < n; k++) {
change(i, j, k);
new_bound = dfs(dv + 1);
if (flg) {
return new_bound;
}
nxt_bound = min(nxt_bound, new_bound);
change(i, i + k -j-1, k);
}
}
}
return nxt_bound;
}
bool id_astar() {
bound = 0;
flg = false;
while(!flg && bound < 5) {
bound = dfs(0);
}
return flg;
}
int main() {
//freopen("in.in", "r", stdin);
int ca; scanf("%d", &ca);
while(ca-- && scanf("%d", &n)) {
for (int i = 0; i < n; i++) {
scanf("%d", shelf + i);
}
if (id_astar() == false) {
puts("5 or more");
} else {
printf("%d\n", bound);
}
}
return 0;
}
Robot
LBOY: 机器人寻路的问题，思路很简单，深搜和广搜都可以，不过这个题目要求强有力的剪枝，一个思路就是启发搜索。
启发函数的设计思路很明显，当前位置距离终点的曼哈顿距离。
但是，题目机器人一次最多可以向前走三步，这里就不能在用搜索树的深度来作为我们要求的实际代价值g()了，因为这样会导致h()不相容。我的h()函数一次最多减小3.那么我一次至少增加三就是了。也对。和上面的一题的思路一样，我们也要配三的方法，g() = depth * 3。 这样h()就是相容的了。可以证明，这是的估价函数可以找到最优解。
#include <iostream>
#include <queue>
using namespace std;
const int stp[4][2] = {
{-1, 0}, {0, 1}, {1, 0}, {0, -1}
}; // n, e, s, w;
const int turn[2] = { 1, -1};
int m, n;
bool mat[50][50];
int f[4][50][50];
int d[4][50][50];
bool c[4][50][50];
int dir[27];
char s[10];
struct node {
int x, y, d;
node(int x=0, int y=0, int d=0)
:x(x), y(y), d(d) {}
bool operator < (const node &p) const {
return f[d][x][y] > f[p.d][p.x][p.y];
}
bool operator == (const node &p) const {
return x == p.x && y == p.y;
}
void out() {
printf("(%d, %d: %d), %d \n", x, y, d, f[d][x][y]);
}
}beg, end, cur;
priority_queue<node> q;
inline bool check(int x, int y) {
if (x <= 0 || x >= m || y <= 0 || y >= n) {
return false;
}
if (mat[x-1][y-1] || mat[x-1][y] || mat[x][y-1] || mat[x][y]) {
return false;
}
return true;
}
inline int dist(int x, int y) {
return abs(x - end.x) + abs(y - end.y);
}
inline void deal(node &cur, int x, int y, int di) {
if (c[di][x][y] == 0) {
c[di][x][y] = 1;
d[di][x][y] = d[cur.d][cur.x][cur.y] + 1;
f[di][x][y] = d[di][x][y] + (dist(x, y) + 2)/3;
q.push(node(x, y, di));
}
else if (c[di][x][y] == 1) {
if (d[di][x][y] > d[cur.d][cur.x][cur.y] + 1) {
d[di][x][y] = d[cur.d][cur.x][cur.y] + 1;
f[di][x][y] = d[di][x][y] + (dist(x, y) + 2)/3;
q.push(node(x, y, di));
}
}
}
int astar() {
if (!check(beg.x, beg.y) || !check(end.x, end.y)) {
return -1;
}
memset(c, 0, sizeof(c));
while(!q.empty()) q.pop();
c[beg.d][beg.x][beg.y] = 1;
d[beg.d][beg.x][beg.y] = 0;
f[beg.d][beg.x][beg.y] = (dist(beg.x, beg.y)+2)/3;
q.push(beg);
int x, y, di;
while(!q.empty()) {
cur = q.top(); q.pop();
if (cur == end) {// cur.out(); //continue;
return d[cur.d][cur.x][cur.y];
}
for (int k = 1; k <= 3; k++) {
x = cur.x + k * stp[cur.d][0];
y = cur.y + k * stp[cur.d][1];
if (check(x, y) == true) {
deal(cur, x, y, cur.d);
} else break;
}
for (int k = 0; k < 2; k++) {
di = (cur.d + turn[k] + 4) % 4;
deal(cur, cur.x, cur.y, di);
}
}
return -1;
}
int main() {
// freopen("in.in", "r", stdin);
dir['n' - 'a'] = 0; dir['e' - 'a'] = 1;
dir['s' - 'a'] = 2; dir['w' - 'a'] = 3;
while(scanf("%d %d", &m, &n) != EOF) {
if (m == 0 && n == 0) break;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", mat[i] + j);
}
}
scanf("%d %d", &beg.x, &beg.y);
scanf("%d %d", &end.x, &end.y);
scanf("%s", s);
beg.d = dir[s[0] - 'a'];
// puts(s); beg.out(); end.out();
printf("%d\n", astar());
}
return 0;
}
周界搜索
LBOY: 结束之前，再引入一个概念，“周界搜索”----当目标状态或者起始状态固定，每次改变的都是另外一个状态的时候，我们就可以用先予处理出，固定状态到其它所有状态的最短路径，这种搜索算法，称为“周界搜索”（引致LRJ的黑皮书P165）
Pushing Boxes
LBOY: 这个是推箱子游戏的简化版，想研究推箱子游戏算法的，可以参考刘如佳的论文《搬运工的启示》，讲解的十分到位。这个题目说的只有一个箱子，一个人，一个目标地点，问用最少的步数将箱子推到目标地点。
题目分析：我们可以一次bfs求出箱子的目标节点到board的每一个小格子的最短距离（广搜第一次到达时候的距离就是最小的）。然后，我们进行启发式搜索，这里我们规定启发函数是 当前位置到目标位置的最短距离。每一步，我们最多推箱子一次，这样，箱子最多往前前进一步，那么估价函数满足单调性，所以这样设计启发函数可以找到最优i解。
代码写的有点长，5k+. 判重的时候我们要记录人和箱子的位置，来进行判重。详细的过程可以参考我的代码：
#include <iostream>
#include <queue>
using namespace std;
int row, col;
char mat[21][21];
int h[21][21];
int d[21][21][21][21];
int f[21][21][21][21];
char c[21][21][21][21];
struct node {
int x1, y1, x2, y2, p, s; // box & man & parent_id
node(int x1=0, int y1=0, int x2=0,int y2=0, int s=0,int p=0)
:x1(x1), y1(y1), x2(x2), y2(y2), s(s), p(p) {}
bool operator < (const node &b) const {
return s == b.s ? f[x1][y1][x2][y2] > f[b.x1][b.y1][b.x2][b.y2]:s > b.s;
}
bool operator == (const node &b) const {
return x1 == b.x1 && y1 == b.y1;
}
void out() {
printf("box:(%d, %d), man:(%d, %d)\n", x1, y1, x2, y2);
}
}start, target;
priority_queue<node> q;
int n;
struct path {
char ch; int p;
void set(char ch, int p) {
this->ch = ch; this->p = p;
}
}p[1<<18];
char ans[1<<10];
struct rnode {
int x, y; // box
rnode(int x=0,int y=0):x(x), y(y) {}
};
queue<rnode> rq;
const int stp[4][2] = {
{-1, 0}, {1, 0}, {0, -1}, {0, 1}
};
const char letter[2][4] = {
{'n', 's', 'w', 'e'},
{'N', 'S', 'W', 'E'}
};
inline bool islegal(int x, int y) {
return x >=0 && x < row && y >= 0 && y < col && mat[x][y] != '#';
}
void bfs(int x, int y) {
memset(h, -1, sizeof(h));
while(!rq.empty()) rq.pop();
rq.push(rnode(x, y));
h[x][y] = 0;
rnode cur;
while(!rq.empty()) {
cur = rq.front(); rq.pop();
for (int k = 0; k < 4; k++) {
x = cur.x + stp[k][0];
y = cur.y + stp[k][1];
if (islegal(x, y) == true) {
if (h[x][y] == -1) {
rq.push(rnode(x, y));
h[x][y] = h[cur.x][cur.y] + 1;
}
}
}
}
}
int astar() {
memset(c, 0, sizeof(c));
while(!q.empty()) q.pop();
n = 0;
c[start.x1][start.y1][start.x2][start.y2] = 1;
d[start.x1][start.y1][start.x2][start.y2] = 0;
f[start.x1][start.y1][start.x2][start.y2] = h[start.x1][start.y1];
p[n].set(0, -1); start.p = 0; start.s = 0; n++;
q.push(start);
node cur;
int x1, y1, x2, y2, s; char ch;
while(!q.empty()) {
cur = q.top(); q.pop();
if (cur == target) {
return cur.p; //d[cur.x1][cur.y1][cur.x2][cur.y2];
}
for (int k = 0; k < 4; k++) { // N, S, W, E
x2 = cur.x2 + stp[k][0];
y2 = cur.y2 + stp[k][1];
if (islegal(x2, y2) == true) {
if (x2 == cur.x1 && y2 == cur.y1) {
x1 = x2 + stp[k][0];
y1 = y2 + stp[k][1];
ch = letter[1][k];
s = cur.s + 1;
} else {
x1 = cur.x1;
y1 = cur.y1;
ch = letter[0][k];
s = cur.s;
}
if (islegal(x1, y1) == true) {
if (c[x1][y1][x2][y2] == 0) { // 未访问
c[x1][y1][x2][y2] = 1; // 插入open
d[x1][y1][x2][y2] = d[cur.x1][cur.y1][cur.x2][cur.y2] + 1;
f[x1][y1][x2][y2] = d[x1][y1][x2][y2] + h[x1][y1];
p[n].set(ch, cur.p);
q.push(node(x1, y1, x2, y2, s, n++));
}
else if (c[x1][y1][x2][y2] == 1) {
if (d[x1][y1][x2][y2] > d[cur.x1][cur.y1][cur.x2][cur.y2] + 1) {
d[x1][y1][x2][y2] = d[cur.x1][cur.y1][cur.x2][cur.y2] + 1;
f[x1][y1][x2][y2] = d[x1][y1][x2][y2] + h[x1][y1];
p[n].set(ch, cur.p);
q.push(node(x1, y1, x2, y2, s, n++));
}
}
}
}
}
}
return -2;
}
int main() {
//freopen("in.in", "r", stdin);
// freopen("out.out", "w", stdout);
int ca = 0;
while(scanf("%d %d", &row, &col) && (row || col)) {
for (int i = 0; i < row; i++) {
scanf("%s", mat + i);
for (int j = 0; j < col; j++) {
if (mat[i][j] == 'B') {
start.x1 = i;
start.y1 = j;
}
if (mat[i][j] == 'S') {
start.x2 = i;
start.y2 = j;
}
if (mat[i][j] == 'T') {
target.x1 = i;
target.y1 = j;
}
}
}
bfs(target.x1, target.y1);
int par = astar();
printf("Maze #%d\n", ++ca);
if (par == -2) {
puts("Impossible.");
} else {
n = 0;
while(par) {
ans[n++] = p[par].ch;
par = p[par].p;
}
while(n--) putchar(ans[n]);
putchar('\n');
}
putchar('\n');
}
}
小结：对于A*和IDA*的文字性总结就到这里，以后遇到好的题目，在继续总结。3Q!
Tags:
文中提及的一些观点和理论，并非全部个人原创，而是自己的总结和心得， 仅供个人学习编程使用！
启发式搜索算法从听说有这个名字开始到正真学习她，应该间隔了一年多的时间吧！当我接触他之后，就有种相见恨晚的感觉！因为她完美的剪枝思想，不仅弥补了通常盲目搜索算法的不足，提高了程序的运行效率，而且给了我一种处理搜索问题的“优化思想”！
下面就让我简单的说一下个人对两种启发式搜索算法，A*和ID_A*算法的理解。开始之前，先推荐比较好的几份资料。
-
《A*算法详解》 Sunway；个人认为他的这篇介绍性的文章写的非常到位，由浅入深的带领我们进入A*算法的世界。强烈建议，学习启发搜索先看这篇文章。（推荐
） - 《A*算法》(ppt) 尚福华； 从理论层面上分析了A*算法的正确性。很值得我们在学了A*算法一段时间之后，回过来分析和思考的。（推荐♦♦♦♦♦）
- 《算法艺术与信息学竞赛》（刘如佳，黄亮 著）P168。介绍的比较笼统，适合有一定基础的人来体会。
先给出一个A*算法的模型Sunway。
Best_First_Search() {
Open = [起始节点S0]; Closed = [NULL];
while (Open表非空) {
从Open中取得一个节点X，并从OPEN表中删除。
if (X是目标节点) {
求得一组最优路径PATH；返回路径PATH；
}
for (每一个X的子节点Y) {
if (Y不在OPEN表和CLOSE表中) {
求Y的估价值；并将Y插入OPEN表中；//还没有排序
}
else
if (Y在OPEN表中) {
if (Y的估价值小于OPEN表的估价值)
更新OPEN表中的估价值；
}
else {//Y在CLOSE表中
if (Y的估价值小于CLOSE表的估价值) {
更新CLOSE表中的估价值；
从CLOSE表中移出节点，并放入OPEN表中；
}
}
}//end for
将X节点插入CLOSE表中；
按照估价值f()将OPEN表中的节点排序；
}//end while
}//end func
谈到A* 算法，就要涉及到三个函数：估价函数f() = 实际代价函数g() + 启发函数 h();
对于状态空间中的某个节点n定义：f*(n)为初始节点src， 约束警告过节点n到达目标节点的最小代价值（f(n)是对f(n)的一个估价，因此成为估价函数）。则f*(n)应包含两部分：一是：从目标节点到达节点N时的最小代价，记为g*() (g() 是g*()的一个上界)；另外一部分是从节点n到达目标节点的最小代价，记为h*(), (因为h()使我们事先无法知晓的，所以，我们用h()来估计，因此，称为估价函数h())。所以，g()是对g*()的一个估价，h()是对h*()的一个估价。
对于实际代价函数g()，我们在搜索到当前节点的时候，有可能最小代价的路径还没有找到，所以 有g() >= g*(), 即 g() 是g*()的一个上界。
对于估价函数g(), 这里要重点介绍一下了，尚福华的ppt里面说的很清晰，这里就引用一下。h(n)的单调限制：
在A*算法中，每当扩展一个节点n时，都需要检查其子节点是否已在Open表或Closed表中。对于那些已在Open表中的子节点，需要决定是否调整指向其父节点的指针；对于那些已在Closed表中的子节点，除了需要决定是否调整其指向父节点的指针外，还需要决定是否调整其子节点的后继节点的父指针。这就增加了搜索的代价。如果我们能够保证，每当扩展一个节点时就已经找到了通往这个节点的最佳路径，就没有必要再去检查其后继节点是否已在Closed表中，原因是Closed表中的节点都已经找到了通往该节点的最佳路径。为满足这一要求，我们需要启发函数h(n)增加单调性限制。
对任意节点ni及其任意子节点nj, 都有 h(ni) <= h(nj) + c(ni, nj); 其中c (ni,,nj)是节点ni到其子节点nj的边代价，则称h(n)满足单调限制。满足此性质的启发函数h()，我们称她是相容（consistent）。
下面是加了H(n)单调性优化的伪代码（黑皮书P170）：
Procedure Expand(State: StateType);
Begin
for i := 1 to OperandCount(State) do
Begin
NewState := DoOperand(State, i);
NewState.h := CalculateH(NewState);
NewState.g := State.g + 1;
NewState.f := NewState.g + NewState.h;
NewState.f := State;
NewState.LastOp := OperandCount;
i := FindInsertTableTwo(NewState); // 在表二中查找，找不到就插入
If i = 0 then
InsertToTableOne(NewState);
ELse if NewState.f < State[i].f then // 新状态优于原状态就替换。
ReplaceInTableOne(NewState, i);
End;
End;
procedure Astar(depth: integer);
begin
Calculate of InitialState;
TableOne := [InitialState]; // 表一：待扩展节点集
TableTwo := [initialState]; // 表二：待扩展和已扩展节点集
ok := false;
while not ok and not TableOne Empty do // 没有找到解且待扩展节点非空
begin
State := ExtractMinInTableOne; // 找f值最小的待扩展节点
If IsAnswer(State) then // 找到解并输出解
Begin
PrintState(state);
ok := true;
End
Else Expand(State); //扩展节点
End;
If not Ok then NoAnswer;
End;
由此， 一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是：
1）搜索树上存在着从起始点到终了点的最优路径。
¤2）问题域是有限的。
¤3）所有结点的子结点的搜索代价值>0。
¤4）h(n)<=h*(n) （h*(n)为实际问题的代价值）。
当此四个条件都满足时，一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法，并一定能找到最优解。简单的来说就两句话：
1. 启发函数是随着深度的增加，是单调不递减的；
2. 估价函数随着深度的增加，也是单调不递减的；
迭代加深+启发函数 = ID_A*
Procedure IDAstar(StartState);
Begin
PathLimit := H(startState) -1; //限定每次搜索的最大深度，初始值为初始状态h();
Success := false;
Repeat
inc(PathLimit);
StartState.g = 0;
Push(OpenStack, StartState);
Repeat
CurrentState := Pop(OpenStack);
If Solution(CurrentState) then // 判定当前状态是否是目的状态
Success = True; // 是的话，玲标记为真。
Else if PathLimit >= CurrentState.g = H(CurrentState) then
ForEach Child(CurrentState) do // 计算所有子状态的f()并入列。
Push(OpenState, Child(CurrentState));
Untill Success or empty of OpenStack
Untill Success or ResourceLimitsReached;
End;
运用迭代加深对深度的限制 和 A*算法的启发函数，结合两个算法的优点，便得到了这个算法。他的优势：
不需要判重（深搜的的特点），省去了hash值设定的烦恼；
不需要排序，省去了堆排序的烦恼，只用到栈，实现简单；
空间的需求较之A*算法，大大减少。因为每次都是规定的最大深度，因此，这个解是最优的。
后记：将在下一节，结合具体的实例，说明这两种算法的好处。并进行一个简单的对比。
Fire station Radar
LBOY: 两个题目是同一个类型，用到的解题思想都是：二分答案 + DLX 判定！以第二个题目为例来说一下。
题目中限制条件，每个消防站可以供应几户人家，如果把消防站看成是行，将用户看成是列，那么问题就是一个“重复覆盖”的模型。因此这里认为每个消防站是和用户相邻的，那么，可以认为用户就是消防站所在地儿。对于给定的最大距离，如果某消防站可以覆盖到某用户，那么就建一个节点。这样构造一个50*50的0-1矩阵。至于最大距离的判断，可以二分来枚举，最大距离，肯定是用户之间的最远距离。但是这样的枚举对于这题是过不去的，需要结构优化：
- 二分枚举长度的时候，枚举已经给定的用户之间的距离。（最后的最长距离也肯定在这里面）这就需要记录下任意两个用户之间的距离，进行排序之后，剔除重复的。然后该枚举长度为枚举长度的下表。
- 如果存在某一列没有消防站覆盖，即d[x].S == 0, 那么直接返回false.因为这样不满足没咧值至少为1的条件。
- 如果M >= N ，那么直接输出0.就可以了。因为每个用户都可以分配到一个用户。
Radar 的优化没用到第一个条件，时间比较长，就补贴了。
link: http://acm.hdu.edu.cn/showproblem.php?pid=3656 http://acm.hdu.edu.cn/showproblem.php?pid=2295
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
#define arr 100
#define brr arr*arr
#define head 0
#define inf 1 << 30
struct Point {
int x, y;
void in() {
scanf("%d %d", &x, &y);
}
int dis2(const Point &p) {
return (x-p.x)*(x-p.x) + (y-p.y)*(y-p.y);
}
}h[arr], f;
struct node {
int S, C;
int R, L, U, D;
}d[brr];
int N, M;
int limit, flg, use[arr];
int dist[arr][arr];
int dis[arr*arr], dn;
int H() {
int ret = 0;
//memset(use, 0, sizeof(use));
for (int i = 0; i <= N+1; i++) use[i] = 0;
for (int t = d[head].R; t != head; t = d[t].R) {
if (use[t] == false) {
use[t] = true; ret ++;
for (int i = d[t].D; i != t; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
use[d[j].C] = true;
// if (d[j].C == head) break;
}
}
}
}
// printf("ret = %d\n", ret);
return ret;
}
void remove(const int &c) {
for (int i = d[c].D; i != c; i = d[i].D) {
d[d[i].L].R = d[i].R;
d[d[i].R].L = d[i].L;
d[d[i].C].S--;
}
}
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
d[d[i].L].R = i;
d[d[i].R].L = i;
d[d[i].C].S++;
}
}
bool dfs(const int &k) {
if (k + H() > M) {
return false;
}
if (d[head].R == head) {
return true;
}
int s = inf, c = 1;
for (int t = d[head].R; t != head; t = d[t].R) {
if(s > d[t].S) {
s = d[t].S;
c = t;
}
}
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return false;
}
bool check(int di) {
d[head].L = N; d[head].R = 1;
for (int j = 1; j <= N; j++) {
d[j].S = 0; d[j].C = j;
d[j].L = j - 1; d[j].R = j + 1;
d[j].U = d[j].D = j;
}
d[N].R = head;
int nod = N, one;
for (int i = 1; i <= N; i++) {
one = nod + 1;
for (int j = 1; j <= N; j++) {
if (dist[i][j] <= di) {
d[j].S++; ++nod; d[nod].C = j;
d[nod].L = nod - 1; d[nod].R = nod + 1;
d[nod].U = d[j].U; d[nod].D = j;
d[d[j].U].D = nod; d[j].U = nod;
}
}
if (one <= nod) {
d[one].L = nod;
d[nod].R = one;
}
}
for (int i = 1; i <= N; i++) {
if (d[i].S == 0) return false;
}
return dfs(0);
}
void bSearch(int mn, int mx) {
int md;
while(mn < mx) {
md = (mn + mx) >> 1;
if (check(dis[md])) {
mx = md ;
} else {
mn = md + 1;
}
}
printf("%lf\n", sqrt(1.0*dis[mx]));
}
int main() {
//freopen("in.in", "r", stdin);
int ca; scanf("%d", &ca);
while(ca-- && scanf("%d %d", &N, &M)) {
dn = 0;
for (int i = 1; i <= N; i++) {
h[i].in();
for (int j = 1; j < i; j++) {
dist[i][j] = dist[j][i] = h[i].dis2(h[j]);
dis[dn++] = dist[i][j];
}
}
if (M >= N) {
printf("%lf\n", 0);
continue;
}
sort(dis, dis + dn);
int k = 0;
for (int i = 1; i < dn; i++) {
if (dis[i] != dis[k]) {
dis[++k] = dis[i];
}
}
bSearch(0, k);
}
return 0;
}
Bomberman - Just Search!
炸弹人游戏，在空地上放置最少的炸弹来炸掉所有的可炸的墙。
先找题目中的限制条件
- 每个炸弹可以放置在空地上，向四个方向爆破，爆破的半径是无限的。
- 每个墙可能被多个炸弹攻击。
- 所有的空地是联通的，也就是说至少存在一组可行解。
上面的第二个条件是重要的，这提示我们用“重复覆盖”的方法来解决，下面要做的就是向重复模型转化了。将每个空位看成行，每个可爆破的墙看成是列。为了方便，我们可以将所有的墙进行列序优先的编号。剩下的就是“套模板”了。
link: http://acm.hdu.edu.cn/showproblem.php?pid=3529
#include <iostream>
using namespace std;
#define arr 225
#define brr arr*arr
#define head 0
#define inf 1 << 30
struct node {
int S, C;
int R, L, U, D;
}d[brr];
int n, m, M;
char mat[16][16];
int col[16][16];
void insert(int &nod, int id) {
d[++nod].C = id; d[id].S++;
d[nod].L = nod - 1; d[nod].R = nod + 1;
d[nod].U = d[id].U; d[nod].D = id;
d[d[id].U].D = nod; d[id].U = nod;
}
int stp[4][2] = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
inline bool islegal(int x, int y) {
return x >= 1 && x <= n && y >= 1 && y <= m && mat[x][y] != '*';
}
void insert(int x, int y, int &nod) {
int one = nod + 1, id, nx, ny;
for (int k = 0; k < 4; k++) {
nx = x + stp[k][0];
ny = y + stp[k][1];
id = -1;
while(islegal(nx, ny) == true) {
if (mat[nx][ny] == '#') {
id = col[nx][ny];
break;
}
nx = nx + stp[k][0];
ny = ny + stp[k][1];
}
if (id != -1) {
insert(nod, id);
// printf("(%d, %d)->(%d, %d)\n", x, y, nx, ny);
}
}
if (one <= nod) {
d[one].L = nod;
d[nod].R = one;
}
}
int limit, use[arr];
int h() {
int ret = 0;
memset(use, 0, sizeof(use));
for (int t = d[head].R; t != head; t = d[t].R) {
if (use[t] == false) {
use[t] = true; ret ++;
for (int i = d[t].D; i != t; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
use[d[j].C] = true;
}
}
}
}
// cout << "ret = " << ret << endl;
return ret;
}
void remove(const int &c) {
for (int i = d[c].D; i != c; i = d[i].D) {
d[d[i].R].L = d[i].L;
d[d[i].L].R = d[i].R;
}
}
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
d[d[i].R].L = i;
d[d[i].L].R = i;
}
}
bool dfs(const int &k) {
if (k + h() >= limit) {
return false;
}
if (d[head].R == head) {
if (k < limit) limit = k;
return true;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return false;
}
int main() {
//freopen("in.in", "r", stdin);
while(scanf("%d %d", &n, &m) != EOF) {
M = 0;
for (int i = 1; i <= n; i++) {
scanf("%s", mat[i] + 1);
for (int j = 1; j <= m; j++) {
if(mat[i][j] == '#') {
col[i][j] = ++M;
}
}
}
d[head].L = M; d[head].R = 1;
for (int j = 1; j <= M; j++) {
d[j].L = j - 1; d[j].R = j + 1;
d[j].U = j; d[j].D = j;
d[j].C = 1; d[j].S = 0;
}
d[M].R = head;
int nod = M;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (mat[i][j] == '.') {
insert(i, j, nod);
}
}
}
// printf("nod = %d\n", nod);
limit = h();
while(dfs(0) == false) limit++;
printf("%d\n", limit);
}
return 0;
}
神龙的难题
LBOY: 问题中的限制条件：
- 每个位置都可以放置炸弹
- 每个位置可以被多个爆破
- 每次的攻击范围可认为是将炸弹放置在左上角。
上面的第二个条件使我们要找的，建模+（重复覆盖）。以每个位置为行（1），恶魔所在的位置（进行列序优先的编号）为列。这样得到一个(N*N)*(N*N)的0-1矩阵。
link: http://acm.fzu.edu.cn/problem.php?pid=1686
#include <iostream>
using namespace std;
#define arr 16
#define brr 256
#define crr arr * brr
#define head 0
#define inf 1 << 30
int n, m, N, M, r, c;
int mat[arr][arr];
struct node {
int S, C;
int L, R, U, D;
}d[crr];
int limit, flg, use[brr];
int h() {
int ret = 0;
memset(use, 0, sizeof(use));
for (int t = d[head].R; t != head; t = d[t].R) {
if (use[t] == false) {
use[t] = true; ret ++;
for (int i = d[t].D; i != t; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
use[d[j].C] = true;
}
}
}
}
// printf("ret = %d\n", ret);
return ret;
}
void remove(const int &c) {
for (int i = d[c].D; i != c; i = d[i].D) {
d[d[i].L].R = d[i].R;
d[d[i].R].L = d[i].L;
}
}
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
d[d[i].L].R = i;
d[d[i].R].L = i;
}
}
int dfs(const int &k) {
if (k + h() > limit) {
return k + h();
}
if (d[head].R == head) {
flg = true;
return k;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if(s > d[t].S) {
s = d[t].S;
c = t;
}
} //printf("k = %d\n", k);
int tmp, nxt = inf;
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
tmp = dfs(k + 1);
if (flg == true) {
return tmp;
}
nxt = min(nxt, tmp);
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return nxt;
}
int id_astar() {
limit = h();
flg = false;
while(flg == false) {
limit = dfs(0);
// printf("limit = %d\n", limit);
}
return limit;
}
int main() {
while(scanf("%d %d", &n, &m) != EOF) {
M = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", mat[i] + j);
if (mat[i][j] == 1) {
mat[i][j] = -(++M);
}
}
}
scanf("%d %d", &r, &c);
d[head].L = M; d[head].R = 1;
for (int j = 1; j <= M; j++) {
d[j].S = 0; d[j].C = j;
d[j].L = j - 1; d[j].R = j + 1;
d[j].U = d[j].D = j;
}
d[M].R = head;
int nod = M, one, id;
for (int i = 1; i <= n - r + 1; i++) {
for (int j = 1; j <= m - c + 1; j++) {
one = nod + 1;
for (int p = i; p < i + r; p++) {
for (int q = j; q < j + c; q++) {
if (mat[p][q] < 0) {
id = -mat[p][q];
d[id].S++; ++nod; d[nod].C = id;
d[nod].L = nod - 1; d[nod].R = nod + 1;
d[nod].U = d[id].U; d[nod].D = id;
d[d[id].U].D = nod; d[id].U = nod;
}
}
}
if (one <= nod) {
d[one].L = nod;
d[nod].R = one;
}
}
}
printf("%d\n", id_astar());
}
return 0;
}
Tags:
文中提及的一些观点和理论，并非全部个人原创，而是自己的总结和心得， 仅供个人学习编程使用！
Dancing Links（DLX），又 被直译为“神奇的舞蹈链”，本质是一个“双向十字循环链表”！是由斯坦福大学的康纳德 E.Knuth在2000年左右提出的一个解决一种NPC问题的算法！对我们acm的竞赛来说，在处理一类搜索问题时，十分有用。
先分享一下学习这种算法比较好的几份资料：
1. 《Dancing Links》 （Donald E. Knuth）本人的论文。英文版的，也有中文的，而且翻译的也很到位: http://sqybi.com/works/dlxcn/#p11#p11
2.《Dancing Links在搜索中的应用》 （momodi）momodi的这篇文章比较系统的讲述了dlx的原理及处理Exact Cover Problem 和 重复覆盖的方法。
依据做过的题目的特点，在简单描述过dlx的插入和删除的方法之后，结合相应的题目，讲一下自己对“完美覆盖（棋盘问题，数独（sudoku）问题，N皇后问题）” 和 “重复覆盖”的理解。
dlx的节点的存储结构：用结构体来表示：
struct node {
int S, C; // size->列链表中节点的总数; column-> 列链表头指针；
int L, R; // left->左向指针， right-> 右向指针; 左右方向
int U, D; // up-> 上向指针， down-> 下向指针；上下方向
};
dlx的节点的删除
void remove(const int&c) {
// column's deleted
d[d[c].L].R = d[c].R;
d[d[c].R].L = d[c].L;
// row's deleted
d[d[c].U].D = d[c].D;
d[d[c].D].U = d[c].U;
}
dlx的节点的恢复
void resume(const int &c) {
// column's resume, d指向的节点要保留原有的信息，
d[d[c].L].R = c;
d[d[c].R].L = c;
// row's resume, d指向的节点要保留原有的信息
d[d[c].U].D = c;
d[d[c].D].U = c;
}
除此之外，为了遍历的方便，要设置一个总的头节点的head!
完美覆盖（精确覆盖）模型
给定一个0-1矩阵，现在要选择一些行，使得一列有且仅有一个 1，如下左：
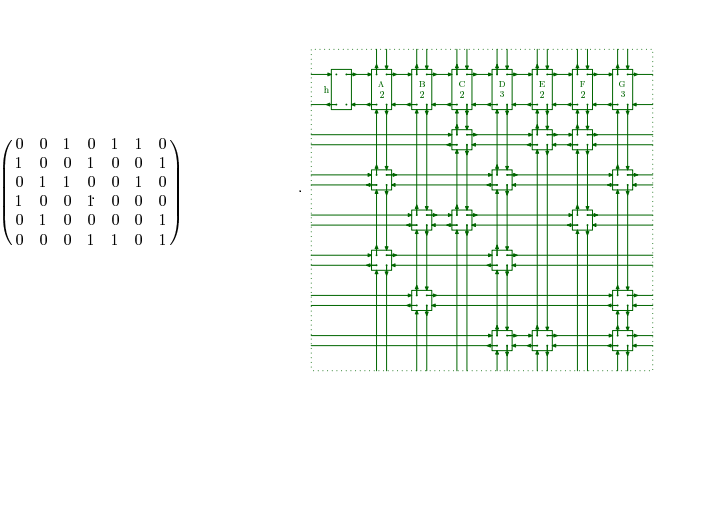
取行集合｛1， 4， 5｝便可以使得每一列仅有一个1。如果我们把行集合｛2， 3， 6｝删掉，并用不同的染色将剩余的行中列为1的标记出来，那么就会得到一个一个完全覆盖的board。这也是这个题目的算法的大体思路：任意选择一列（这里我们先选择任意一列，待会再说如何优化），选择为1的一行，然后将该从该行中找出所有的节点值为1的节点，将这些节点所在的列中节点为值为1的行删除掉，这样我们就可以保证选择了改行之后，保证每列中只有一个1。 这样将所有的行试探之后，如果最后存在一种可以使得原矩阵为空的方案，那么就找到一组解。下面简单说一下对优化（即，每次选择剩余列中元素个数最少的来删除）的理解，
我们优化的出发点是选择尽量少的行找到一组可行解，按照我们上面的思路就是选择一行的同时尽量多的删除其它的行。由此，列的值（多少代表着影响的行数）大的删掉的行数也就越多，那么就更大的可能接近可行解。（只是论述，缺乏严密的数学证明）（更为具体的分析，参见momodi的论文P4，下面附上一段伪代码,帮助理解）
A is the matrix of the 0-1.
if (A is empty) {
\\A is the 0 - 1 matrix.
the problem is solved;
return;
}
choose a column, c,that is unremoved and has fewest elements. ..(1)
remove c and each row i that A[i][c] == 1 from matrix A;...(2)
for (all row, r, that A[r][c] == 1) {
include r in the partial solution.;
for each j that A[r][j] == 1 {
remove column j and each row i
that A[i][j] == 1 from matrix A. ...(3)
}
repeat this algorithm recursively on the reduced matrix A.
resume all column j and row i that was just removed;...(4)
}
resume c and i we removed at step(2) ...(5);
完美覆盖的cpp实现。
// resumecolumn c and all row i that a[i][c] = 1;
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
for (int j = d[i].L; j != i; j = d[j].L) {
d[d[j].C].S++;
d[d[j].U].D = j;
d[d[j].D].U = j;
}
}
d[d[c].R].L = c;
d[d[c].L].R = c;
}
// the k'th step of the deepth first search;
bool dfs(const int &k) {
if (d[head] == head) {
return true;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
remove(c);
for (int i = d[c].D; i != c; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
remove(d[j].C);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(d[j].C);
}
}
resume(c);
return false;
}
重复覆盖模型：在0-1矩阵中选择最少的行，是的每一列至少有一个1.
该问题可以想象成二分图的支配集问题的模型：从X集合选择最少的点，是的能否覆盖住Y集合所有的点。（当然X与Y集合是有边（映射）关系的）。
把这个问题和上面的完美覆盖结合起来看，我们就会发现不同的地方就是，上面红色标出的那句话，实际上也是如此。能够想到的一个中直观的搜索方法是：我们每次选择任意选一列，然后从该列选择任意一行，同时将列值为1的节点所在的列删掉（这里不再是将列上值为1的节点所在的行删掉，因为不再要求列值为1）。如果，最后的所有的列都删掉了，那么就可以说找到一组可行解。
这个题目的做法是用迭代加深的启发式搜索（ID_A*)。那么，我们来说一下启发函数的设计。
int h() {
int ret = 0;
memset(use, 0, sizeof(use));
for (int t = d[head].R; t != head; t = d[t].R) {
if (use[t] == false) {
use[t] = true; ret ++;
for (int i = d[t].D; i != t; i = d[i].D) {
for (int j = d[i].R; j != i; j = d[j].R) {
use[d[j].C] = true;
}
}
}
}
return ret;
}
启发函数的值 = 按一定的规则选择列，是的所有的列都被选择需要的最少的行数。（这里的按一定的规则是说，每次开始选择列的时候都遵守一个规则）。说明估价函数（f() = g() + h()）发函数的正确性,我们只需要说明两点：1. f（）满足单调不减的特性； 2. h()是相容的，也就是说,设pres, curs 为前一个状态和当前状态，weight为状态转移代价，那么h(pres) <= curs + weight。 按通常的dfs的估价函数设计的方法，去实际代价函数g（） = depth of the search. 那么 g()函数值每只增加一个单位“1”。对于h()函数，按照f的不递减的特性，需要满足每次减少的最大值为“1"才可。 如果按照我们我们上面启发函数的设计原则，每次计算的时候记录下计算估价函数值时用到的列，那么，对于当前的此次计算挂架函数值，会出现两种情况，一是，原来记录下的列有被删除的（每次只能删除一个原来记录的列，因为，记录的列之间是没有关系的），这样h（）的函数值减小一；二是，原来记录的列没有被删除的，这样h()的函数值保持不变。由此，weight = 0 或 1，h() 函数是相容的，f() = g() + h() 满足单调不递减的特性。
简单的来说，对于重复覆盖，我们只删除列，不删除行。由此得到以下的cpp重复覆盖的代码（供参考）
void remove(const int &c) {
for (int i = d[c].D; i != c; i = d[i].D) {
d[d[i].R].L = d[i].L;
d[d[i].L].R = d[i].R;
}
}
void resume(const int &c) {
for (int i = d[c].U; i != c; i = d[i].U) {
d[d[i].R].L = i;
d[d[i].L].R = i;
}
}
bool dfs(const int &k) {
if (k + h() >= limit) {
return false;
}
if (d[head].R == head) {
if (k < limit) limit = k;
return true;
}
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
if (dfs(k + 1)) {
return true;
}
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return false;
}
int astar() {
limit = h();
while(dfs(0) == false) limit++;
return limit;
}
对于ID_A*,我个人比较喜欢下面的这种实现方法：
int dfs(const int &k) {
if (k + h() > limit) {
return k + h();
}
if (d[head].R == head) {
flg = true;
//if (k < limit) limit = k;
return k;
}
// printf("k = %d\n", k);
int s = inf, c;
for (int t = d[head].R; t != head; t = d[t].R) {
if (s > d[t].S) {
s = d[t].S;
c = t;
}
}
int nxt = inf, tmp;
for (int i = d[c].D; i != c; i = d[i].D) {
remove(i);
for (int j = d[i].R; j != i; j = d[j].R) {
remove(j);
}
tmp = dfs(k + 1);
if (flg == true) {
return tmp;
}
nxt = min(nxt, tmp);
for (int j = d[i].L; j != i; j = d[j].L) {
resume(j);
}
resume(i);
}
return nxt;
}
Tags: Dancing Links
Copyright © 2007